Quantum dynamics is the study of quantum effects in the motion of atoms and molecules. Dramatic progress has been made in this field recently (by us and other groups around the world), by combining approaches from Feynman path-integral theory with high-performance computing.

Feynman path-integral theory

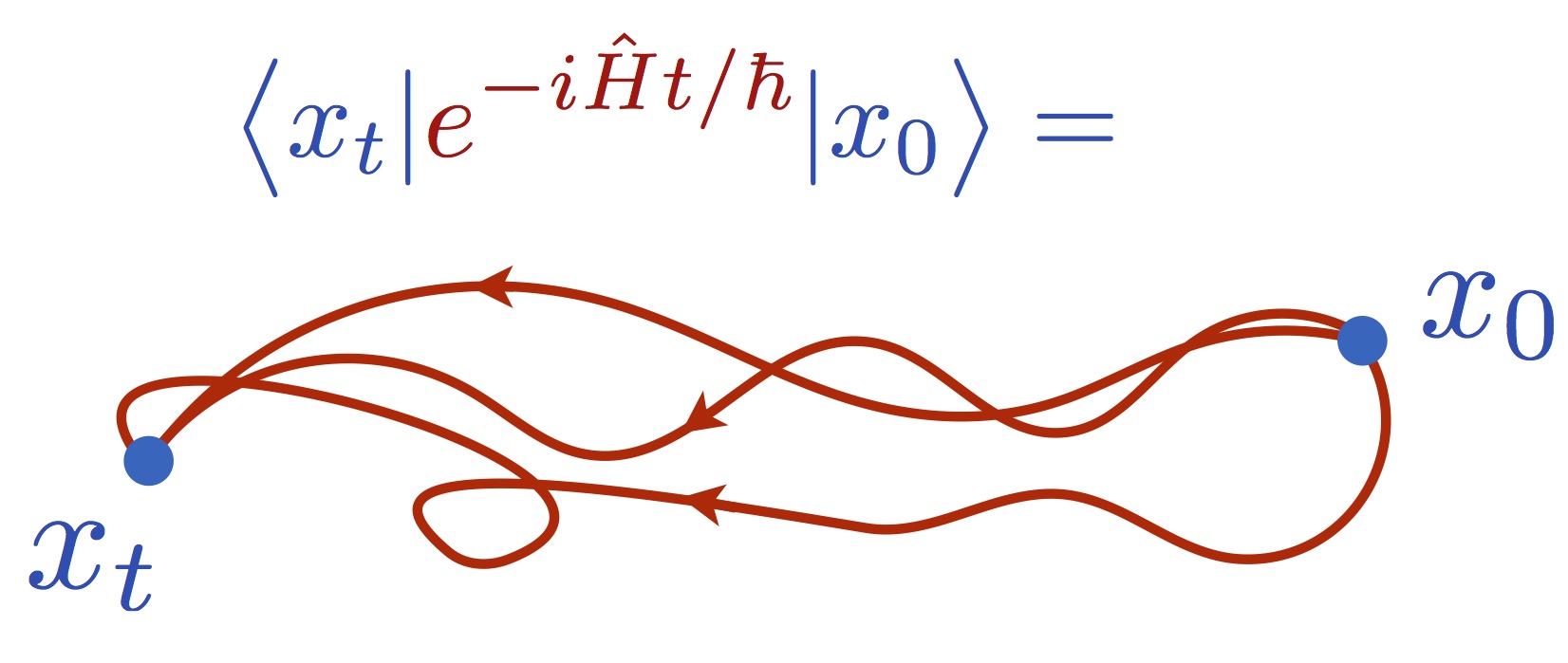Feynman path-integral theory is an alternative, completely rigorous, formulation of quantum theory that uses paths instead of wave functions. The basic idea is to construct matrix elements of the time-evolution operator by summing all possible paths between two points, weighting the paths by the classical action. Remarkably, this gives identical results to solving the Schrödinger equation: see the book by Feynman and Hibbs for more details.

Feynman path-integrals have revolutionized quantum dynamics by sidestepping the need to solve the Schrödinger equation (which is possible only for few-atom systems—see below). This is because, although the space of Feynman paths is impossibly vast for electrons, it is manageable for nuclei, as a result of two special conditions. First, the masses of nuclei are quite heavy, so the de Broglie wavelengths are small: this forces the Feynman paths to keep reasonably close to the classical (i.e. Newtonian paths). Second, most dynamics in chemistry takes place at thermal equilibrium, where the main quantum effects operate indirectly on the dynamics, through the quantum Boltzmann operator.

Ring-polymer representation

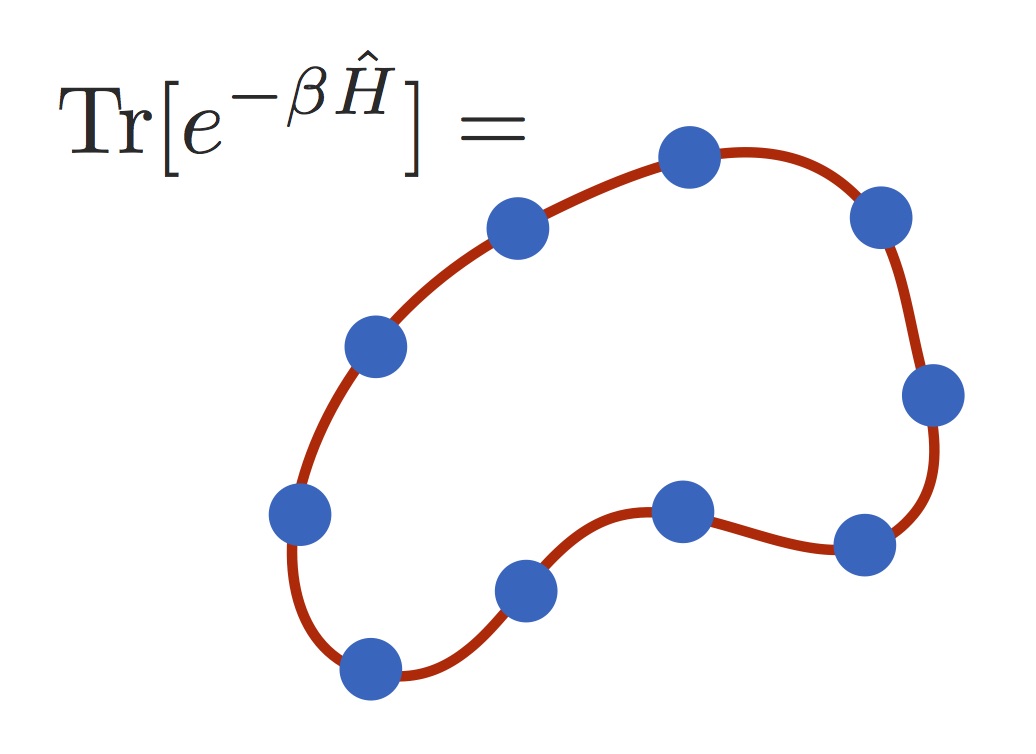The quantum Boltzmann operator has the same form as the time-evolution operator, with the time taking the imaginary value t=-iβℏ, where β=1/kT sets the temperature. This makes the space of Feynman paths easy to sample, because the paths have real weights, and can be represented efficiently using 'ring polymers'—which are not real polymers, but discrete representations of Feynman paths. The ring polymers are closed paths, which represent the delocalisation produced by the quantum Boltzmann operator; they thus collapse to classical point-particles at high temperatures. Ring-polymers have been used for a long time to simulate quantum statistical averages (see e.g. classic papers by Chandler, Wolynes, Ceperley and Parrinello). Recently, however, it has been found that ring-polymers can also be used to simulate quantum dynamics. This is because most quantum dynamical effects at thermal equilibrium are indirect, and arise from quantum effects in the statistics (i.e. the ring-polymers) feeding into the real-time dynamics (which is otherwise classical).

Instantons

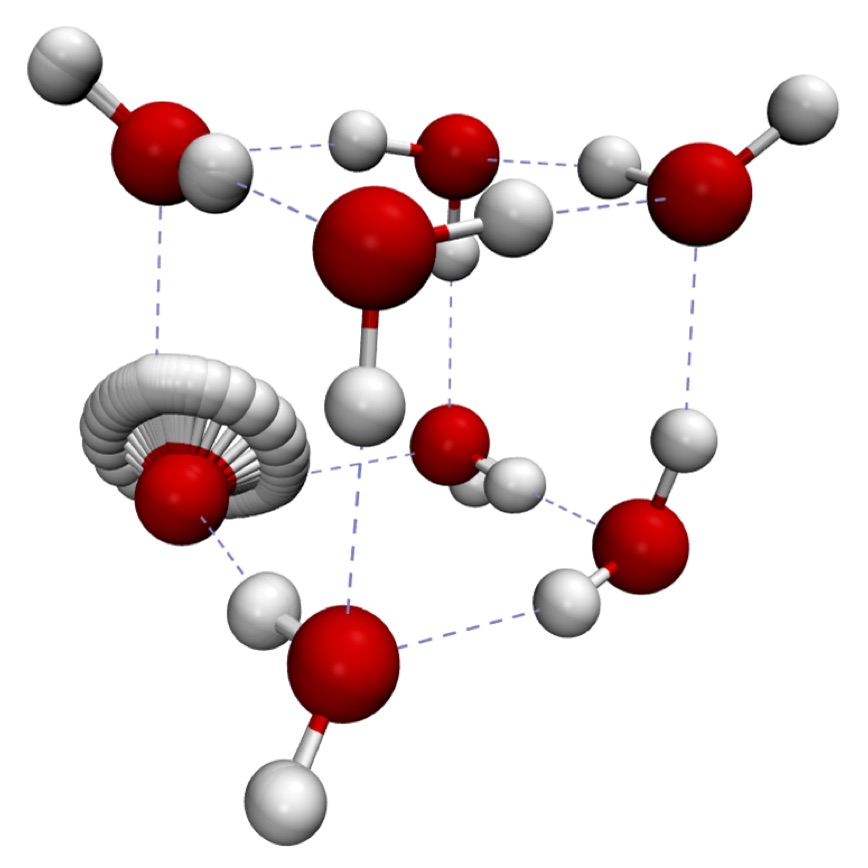Some of these quantum dynamical effects can be extracted straight from the ring-polymers, without the need to evolve the system in real time. One example is when a system quantum-tunnels between equivalent minima. This produces energy-level splittings, which can often be predicted to a good approximation by isolating a single, dominant, Feynman path called the instanton. Using this technique, we can compute tunnelling effects in much larger systems than can be treated by conventional Schrödinger-based quantum techniques. The figure on the right shows an instanton in the water octamer; this is part of a series of studies on water clusters, which we are currently making in collaboration with experimental groups who probe the clusters using terahertz spectroscopy. We are also using instantons to calculate reaction rates in a collaboration involving the Molpro electronic-structure package.

Fully quantum transition-state theory

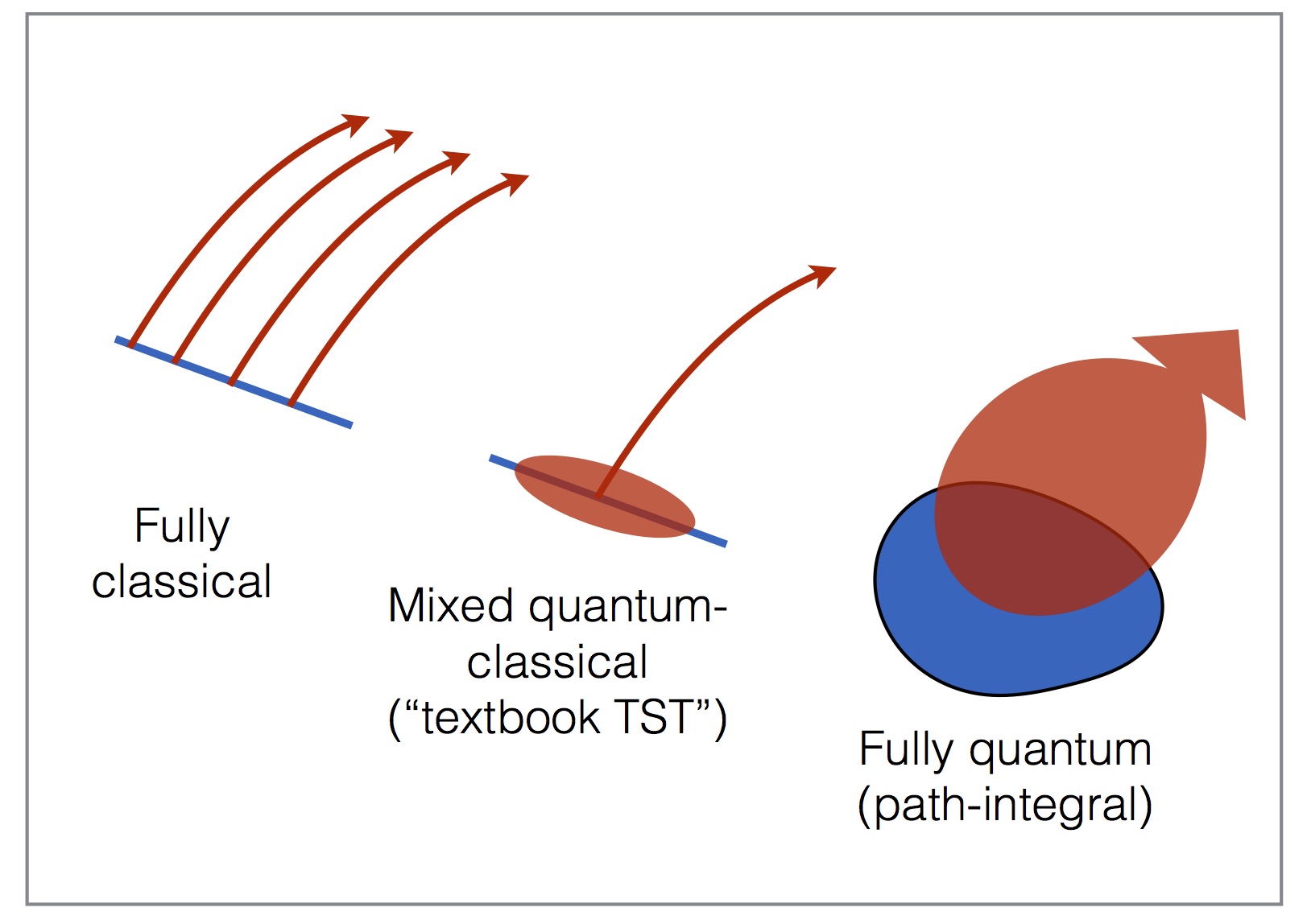Another quantum dynamical property that can be extracted straight from the ring-polymers is the rate of a direct reaction. Such rates are typically calculated using 'textbook' transiton-state theory (TST—as taught to every PhysChem student!), which works well for many systems, but not for reactions involving tunnelling. We have found recently that there exists a fully quantum generalization of transition-state theory, which obtains the rate from a delocalised quantum flux over the reaction barrier (see right). Amazingly, this flux gives a good approximation of the reaction rate even in regimes where quantum tunnelling speeds it up by six orders of magnitude. The tunnelling is contained entirely within the ring-polymers, which have the effect of boosting the flux through (not over!) the barrier. It turns out that a practical method, called ring-polymer molecular dynamics (RPMD), which was previously considered heuristic, gives a good approximation to the quantum TST rate; this method is allowing quantum TST to be applied to proton- and hydrogen-transfer rates in enzyme- and surface-catalyzed reactions.

Matsubara dynamics

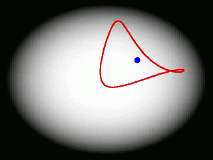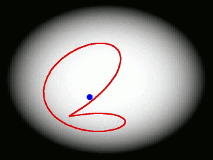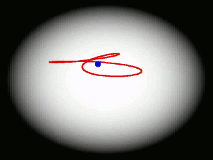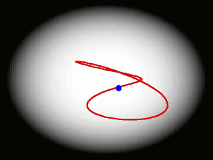One of the main goals of our current research is to develop a completely general theory of quantum dynamics based on the premise that most quantum dynamical effects originate in the ring-polymers (and are then 'fed into' the real-time dynamics of the particles). We have recently derived such a theory; its properties are surprising and can be summarised by a movie (see right). We find that the real-time dynamics of a particle is represented by a loop (which is much floppier than a ring-polymer) which fluctuates around its centre of mass. The loop is completely classical (i.e. Newtonian) in its dynamics, and behaves rather like an elastic band. Its delocalization represents the quantum effects (mainly tunnelling and zero point energy) contained in the quantum Boltzmann operator. This theory, called 'Matsubara dynamics', is completely general and is probably sufficiently quantum mechanical to describe accurately a wide range of quantum dynamical observables (e.g. the spectra of liquids, non-direct reaction rates, neutron-scattering cross sections, diffusion and transport properties). We are currently developing practical ways to implement Matsubara dynamics.

Complete wave functions of simple reactions

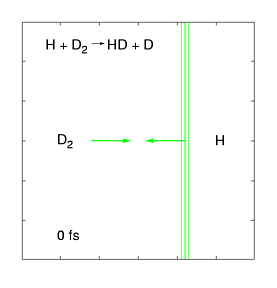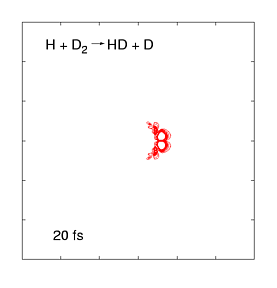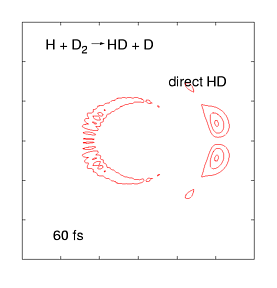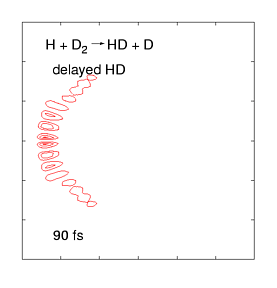The quantum dynamics of few-atom systems can be calculated exactly, by solving the Schrödinger equation. The figure (right) shows a wave function obtained by solving the time-dependent Schrödinger equation for one of the simplest chemical reactions (H + D₂ →HD + D). This was the first complete wave function ever calculated of a chemical reaction, showing the products scattering into space in the immediate (100 femtosecond) aftermath of a molecular collision. These wave functions are incredibly complex, even for such a simple reaction, as they contain all probable reaction mechanisms. For the past decade, we have been calculating these wave functions over a wide range of collision energies and preparation conditions, and mapping them onto experimental data measured by the Zare group (who use molecular beam tools to effectively measure |Ψ|² as the products fly into space). This work has uncovered some weird quantum effects as well as (reassuringly) showing that most of the wave function describes respectable chemistry.

Key references

• 1. Ring-polymer molecular dynamics rate-theory in the deep-tunneling regime, J. Chem. Phys. 131, 214106 (2009)
• 2. Ring-polymer instanton method for calculating tunneling splittings, J. Chem. Phys. 134, 054109 (2011)
• 3. Seemingly Anomalous Angular Distributions in H + D₂ Reactive Scattering, Science 336, 1687 (2012)
• 4. Derivation of a true quantum transition-state theory, J. Chem. Phys. 138, 084108 (2013)
• 5. Is the simplest chemical reaction really so simple? PNAS 111, 15 (2014)
• 6. Boltzmann-conserving classical dynamics in quantum time-correlation functions, J. Chem. Phys. 142, 134103 (2015)
• 7. Communication: Relation of centroid molecular dynamics and ring-polymer molecular dynamics to exact quantum dynamics, J. Chem. Phys. 142, 191101 (2015)
• 8. Concerted hydrogen-bond breaking by quantum tunneling in the water hexamer prism, Science 351, 1310 (2016)